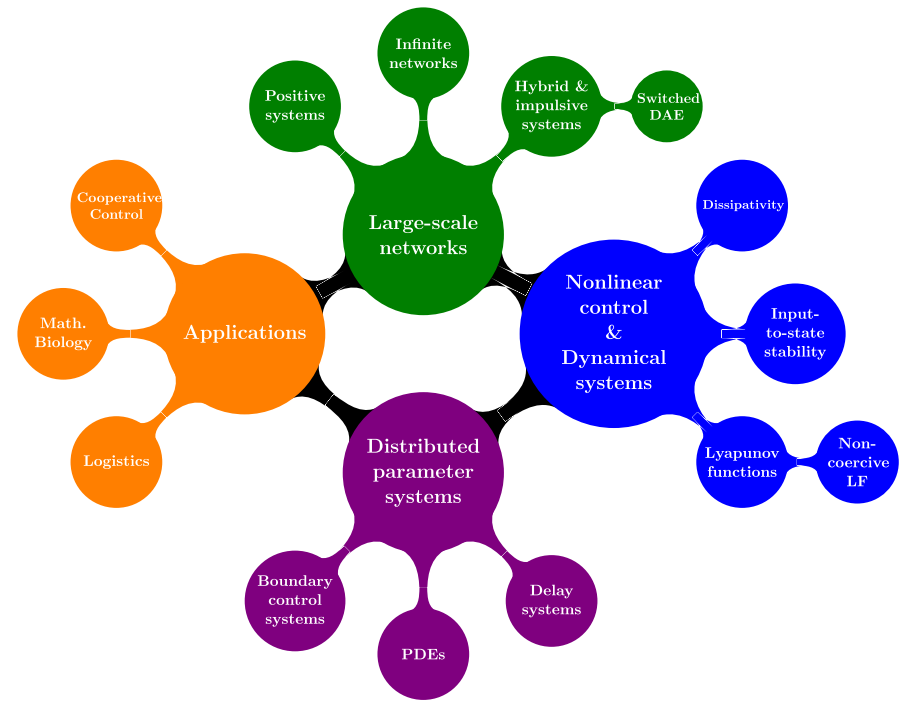
Research Interests
My research interests lie mainly in control and dynamical systems theory of finite and infinite dimensional systems and in its applications to logistics and biology.
More specifically, I am interested in:
Input-to-state stability and control of nonlinear systems
Infinite-dimensional systems
Large-scale networks
Hybrid systems (in particular, impulsive and switched systems)
Time-delay systems
Life history evolution and optimal allocation models of plants
Input-to-state stability and control of nonlinear systems
The notion of input-to-state stability (ISS) has been introduced by
E. Sontag in 1989. It combines two different types of stability behavior:
Stability in the sense of Lyapunov and input-output stability.
The unified treatment of external and internal stability has made ISS a
the central tool in robust stability analysis of nonlinear control systems.
ISS plays an essential role in constructive nonlinear control; in particular,
in robust stabilization of nonlinear systems, stabilization via controllers
with saturation, design of robust nonlinear observers, nonlinear detectability,
ISS feedback redesign, stability of nonlinear networked control systems,
supervisory adaptive control and others.
In recent years, interest in this theory has been growing rapidly because of
modern attempts to control processes described by PDEs. On the other hand,
several effective stabilization methods for
infinite-dimensional systems have been proposed during the last decade, such as continuum backstepping,
stabilizer design for port-Hamiltonian systems, etc. This paves the way for
the development of robust stabilization methods for infinite-dimensional
systems provided that another prerequisite is available: the theory of
ISS for distributed parameter systems. Thus, a solid theoretical background
for ISS theory of distributed parameter systems is needed from the viewpoint
of ISS theory itself, as well as in view of applications.
One of my research goals is to develop such a comprehensive theory, including its foundations and applications to the robust stabilization of PDEs.
Infinite-dimensional systems
Partial differential equations describe processes in which temporal as well as spatial derivatives of the state variables are included
in the description of the dynamics. Equations of this kind arise in
the modeling of many physical, chemical, or biological processes.
They are also used in the analysis of communication networks, image processing, and logistics. Famous examples are the Maxwell equations of electrodynamics
as well as wave and heat equations describing various propagation processes.
Partial differential equations are an example of infinite-dimensional systems.
We are interested in the dynamics of such systems under the influence of
external disturbances and/or control inputs.
The study of interconnections plays a significant role in the
mathematical systems theory, as it allows one to establish stability
for a complex system based on the properties of its less complex components.
In this context, small-gain theorems prove to be useful and general
in analyzing feedback interconnections of nonlinear systems, which are ubiquitous in the control
literature.
The general idea of small-gain analysis is to decompose a network into stable
components that have a certain degree of robustness
against the inputs coming from other subsystems.
Then, if the destabilizing influence of subsystems on each other is 'not too strong' (which is expressed by a so-called small-gain condition), then the whole network is stable.
These important results have been obtained for finite networks of finite-dimensional subsystems
in the 1990s and 2000s.
However, in modern applications of control theory, we are interested in networks
whose components may be infinite-dimensional systems, such as delay systems or partial differential equations.
On the other hand, recent advances in large-scale computing, cheap distributed sensing,
and large-scale data management have created the potential for smart applications
in which large numbers of dispersed agents need to be regulated for a common objective.
For instance, in smart cities, city-wide traffic control based on cheap personal
communication, car-to-car communication, and the deployment of numerous sensors
can provide a significant step toward safe, energy-efficient, and environmentally friendly traffic concepts.
In my research, I have shown that (after a proper modification) the small-gain methods
can be applied to finite and infinite networks of control systems with
possibly infinite-dimensional components.
In this generality, the result covers the most important control systems arising in applications.
Hybrid systems (in particular, impulsive and switched systems)
In the modeling of real phenomena, one often has to consider systems that
exhibit both continuous and discontinuous behavior.
Examples of such systems are networks that contain both analog and digital components,
as well as mechanical devices controlled by digital controllers.
A systematic framework for such systems is the hybrid systems theory.
A special case of hybrid systems in which the discrete jumps occur only at some
prescribed moments (that do not depend on the state of the system)
are called impulsive systems.
Stability and control of hybrid systems is one of the central topics in a
modern control theory.
I am interested in the study of the stability and robustness of such systems,
as well as in the analysis of networks with hybrid components, whose subsystems may have unstable discrete
and/or continuous behavior.
In many applications, the evolution of the system depends not only on the current value of the solution map
but also on its past values. Applications include control under communication and transmission delays,
teleoperator systems, aerospace engineering, etc.
In my research, I study Lyapunov-Krasovskii method for stability analysis of delay systems,
input-to-state stability of nonlinear time-delay systems,
as well as properties of reachability sets of such systems.
Life history evolution and optimal allocation models of plants
Consider a plant as a system consisting of a number of compartments –
at least of a vegetative compartment (leaves, roots, stems) and a
reproductive compartment (seeds and auxiliary tissues), although
storage and defensive tissues could also be included.
In optimal allocation models, it is assumed that a plant is 'smart.'
Namely, a plant is considered as a self-controlled system that can
control its resource allocation to maximize its fitness, which
is often identified with the mass of seeds produced by a plant
during its lifetime.
Usually, the models of annual plants and of perennial plants are considered separately.
I have developed a model that allows successfully analyzing
annual plants with single or multiple reproduction periods, monocarps, evergreen perennials, and polycarpic perennials in a unified way.